Invariance Learning in Deep Neural Networks with Differentiable Laplace Approximations
Abstract
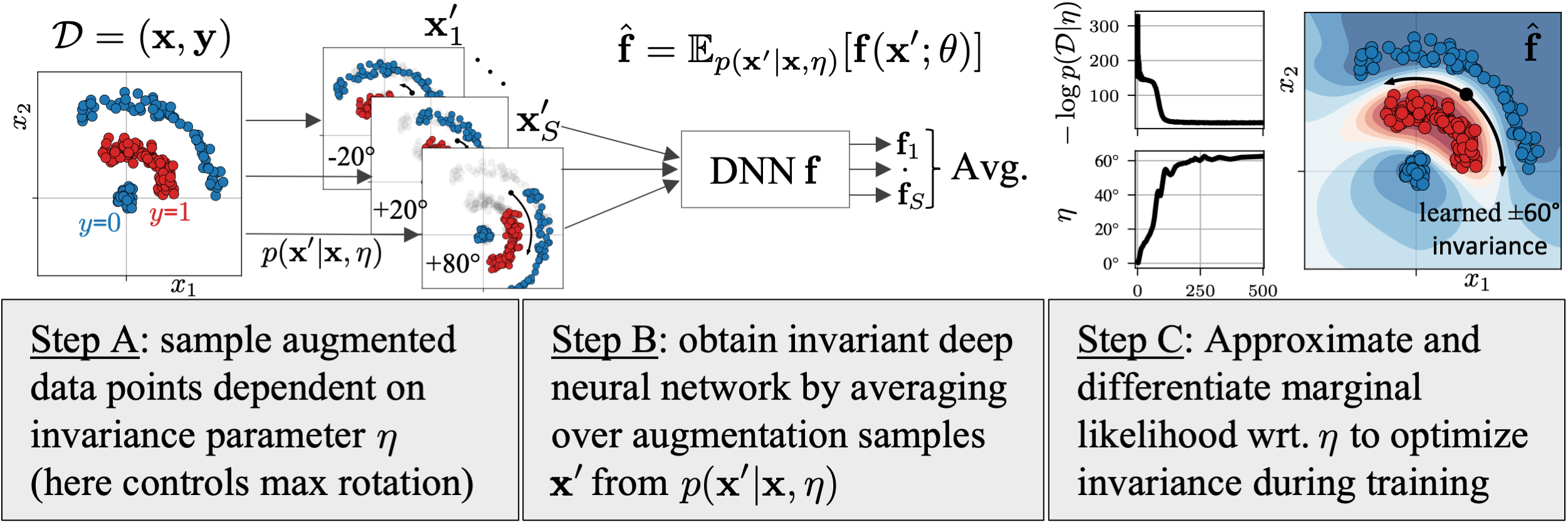
Data augmentation is commonly applied to improve performance of deep learning by enforcing the knowledge that certain transformations on the input preserve the output. Currently, the correct data augmentation is chosen by human effort and costly cross-validation, which makes it cumbersome to apply to new datasets. We develop a convenient gradient-based method for selecting the data augmentation. Our approach relies on phrasing data augmentation as an invariance in the prior distribution and learning it using Bayesian model selection, which has been shown to work in Gaussian processes, but not yet for deep neural networks. We use a differentiable Kronecker-factored Laplace approximation to the marginal likelihood as our objective, which can be optimised without human supervision or validation data. We show that our method can successfully recover invariances present in the data, and that this improves generalisation on image datasets.
Links
 Alexander Immer
Alexander Immer