Improving predictions of Bayesian neural networks via local linearization

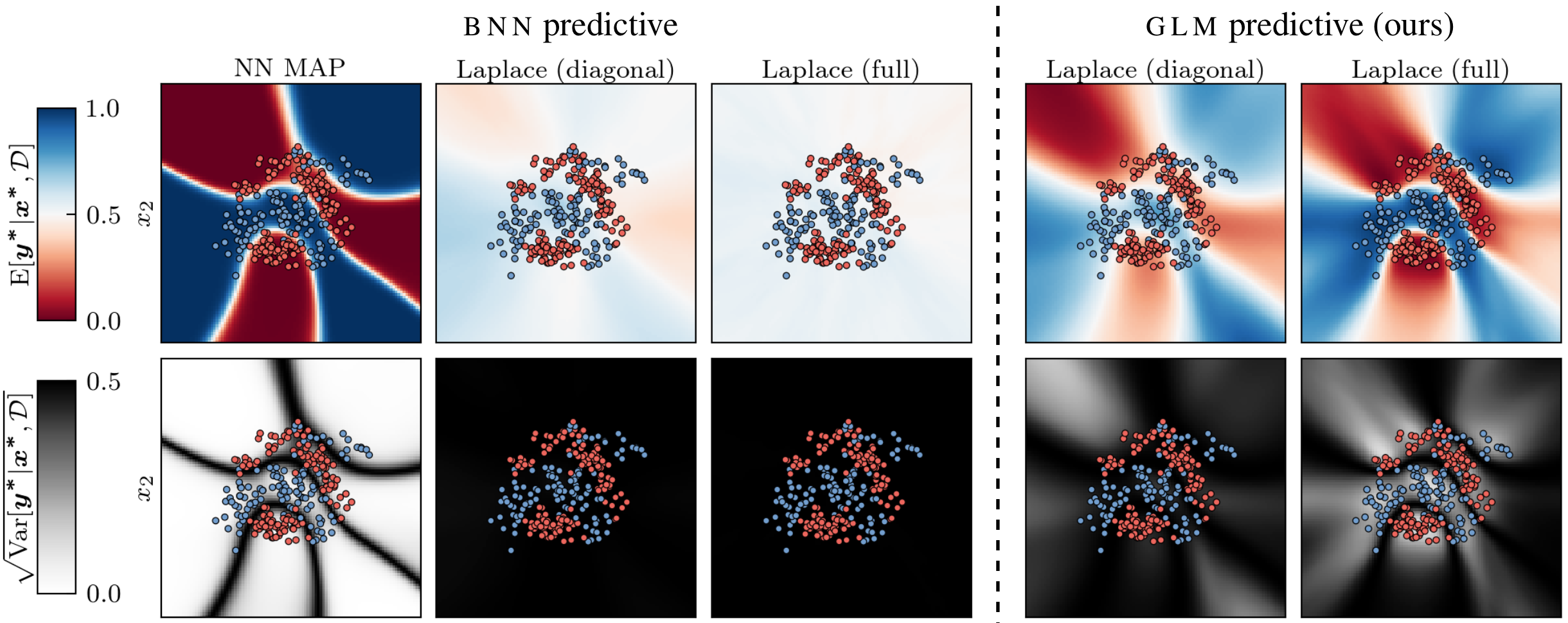
The generalized Gauss-Newton (GGN) approximation is often used to make practical Bayesian deep learning approaches scalable by replacing a second order derivative with a product of first order derivatives. In this paper we argue that the GGN approximation should be understood as a local linearization of the underlying Bayesian neural network (BNN), which turns the BNN into a generalized linear model (GLM). Because we use this linearized model for posterior inference, we should also predict using this modified model instead of the original one. We refer to this modified predictive as “GLM predictive” and show that it effectively resolves common underfitting problems of the Laplace approximation. It extends previous results in this vein to general likelihoods and has an equivalent Gaussian process formulation, which enables alternative inference schemes for BNNs in function space. We demonstrate the effectiveness of our approach on several standard classification datasets and on out-of-distribution detection.