Disentangling the Gauss-Newton Method and Approximate Inference for Neural Networks

Deep neural networks achieve state-of-the-art performance in many real-world machine learning problems and alleviate the need to design features by hand. However, their flexibility often comes at a cost. Neural network models are hard to interpret, often overconfident, and do not quantify how probable they are given a dataset. The Bayesian approach to infer neural networks is one way to tackle these issues. However, exact Bayesian inference for neural networks is intractable. Therefore, Bayesian deep learning combines approximate inference and optimization methods to design efficient methods that provide an approximate solution. Nonetheless, the combination of both methods is often not well understood.

In this thesis, we disentangle the generalized Gauss-Newton and approximate inference for Bayesian deep learning. The generalized Gauss-Newton method is an optimization method that is used in several popular Bayesian deep learning algorithms. In particular, algorithms that combine the Gauss-Newton method with the Laplace and Gaussian variational approximation have recently led to state-of-the-art results in Bayesian deep learning. While the Laplace and Gaussian variational approximation have been studied extensively, their interplay with the Gauss-Newton method remains unclear. For example, we know that both approximate inference methods compute a Gaussian approximation to the posterior. However, it is not clear how the Gauss-Newton method impacts the underlying probabilistic model or posterior approximation. Additionally, recent criticism of priors and posterior approximations in Bayesian deep learning further urges the need for a deeper understanding of practical algorithms.

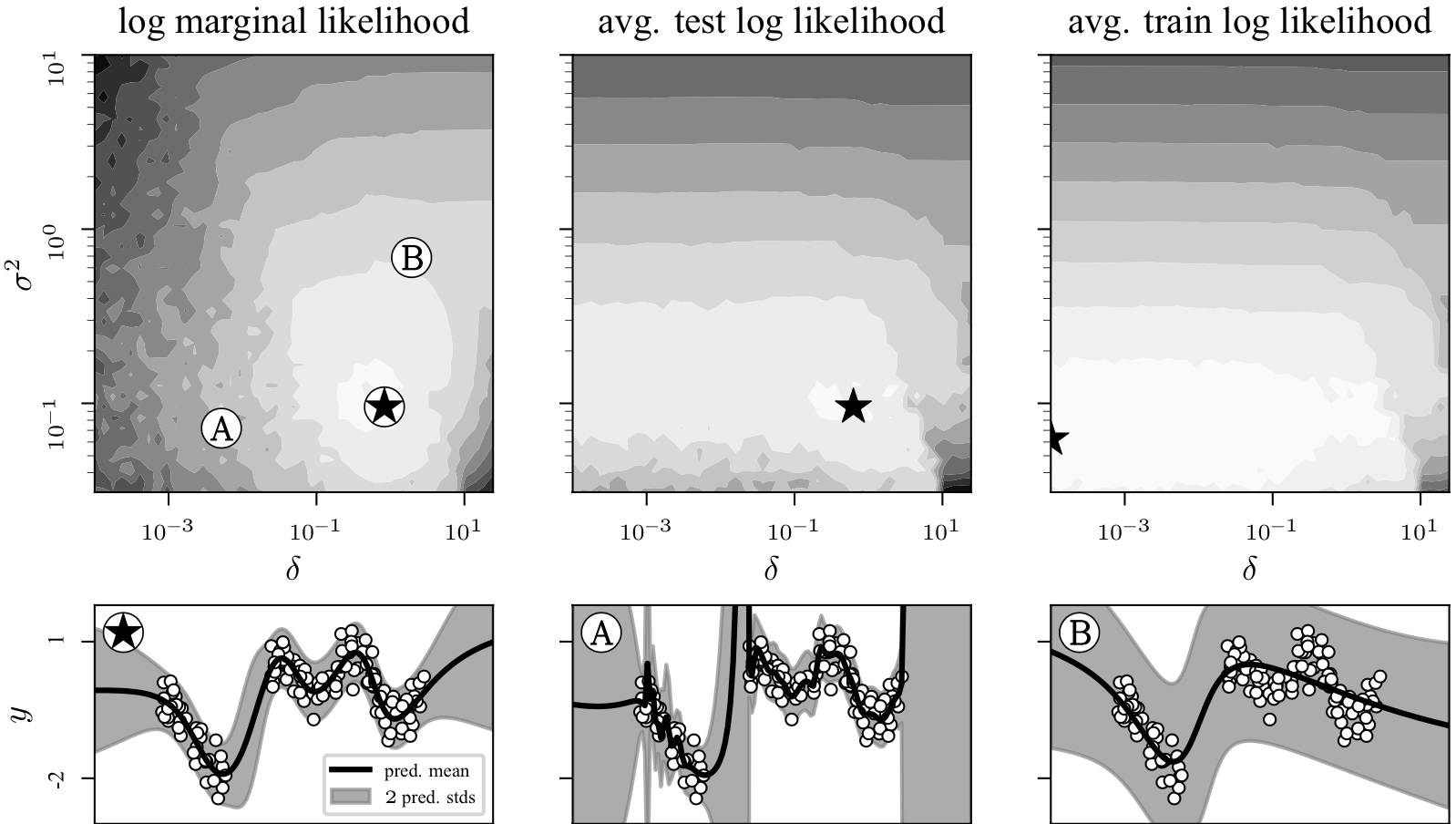
The individual analysis of the Gauss-Newton method and Laplace and Gaussian variational approximations for neural networks provides both theoretical insight and new practical algorithms. We find that the Gauss-Newton method simplifies the underlying probabilistic model significantly. In particular, the combination of the Gauss-Newton method with approximate inference can be cast as inference in a linear or Gaussian process model. We find that the Gauss-Newton method turns the original model locally into a linear or Gaussian process model. The Laplace and Gaussian variational approximation can subsequently provide a posterior approximation to these simplified models. This new disentangled understanding of recent Bayesian deep learning algorithms also leads to new methods: first, the connection to Gaussian processes enables new function-space inference algorithms. Second, we present a marginal likelihood approximation of the underlying probabilistic model to tune neural network hyperparameters. Finally, the identified underlying models lead to different methods to compute predictive distributions. In fact, we find that these prediction methods for Bayesian neural networks often work better than the default choice and solve a common issue with the Laplace approximation.