Variational Inference with Numerical Derivatives: Variance Reduction through Coupling

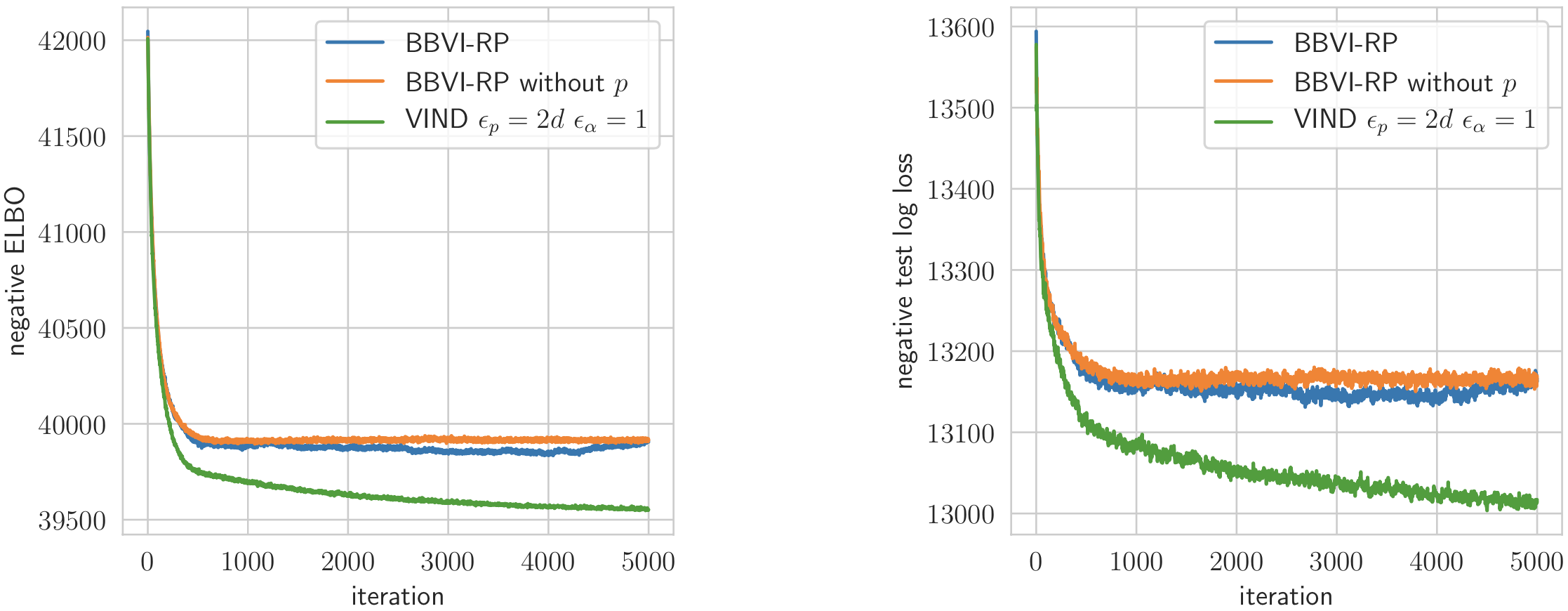
Black Box Variational Inference provides a universal method for Variational Inference, but taking advantage of special properties of the approximation family or of the target can improve the convergence speed significantly. For example, if the approximation family is a transformation family, such as a Gaussian, then switching to the reparameterization gradient often yields a major reduction in gradient variance. Ultimately, reducing the variance can reduce the computational cost and yield better approximations.

We present a new method to extend the reparameterization trick to more general exponential families including the Wishart, Gamma, and Student distributions. Variational Inference with Numerical Derivatives (VIND) approximates the gradient with numerical derivatives and reduces its variance using a tight coupling of the approximation family. The resulting algorithm is simple to implement and can profit from widely known couplings. Our experiments confirm that VIND effectively decreases the gradient variance and therefore improves the posterior approximation in relevant cases. It thus provides an efficient yet simple Variational Inference method for computing non-Gaussian approximations.